I have come across hard problem in leetcode where modified bucket-sort need to be applied. It is good example how bucket-sort can be applied to resolve the problem quite easily.
Problem Definition
Problem definition goes as follows:
Given an integer array nums, return the maximum difference between two successive elements in its sorted form. If the array contains less than two elements, return 0.
You must write an algorithm that runs in linear time and uses linear extra space.
Example 1:
Input: nums = [3,6,9,1]
Output: 3
Explanation: The sorted form of the array is [1,3,6,9], either (3,6) or (6,9) has the maximum difference 3.
Example 2:
Input: nums = [10]
Output: 0
Explanation: The array contains less than 2 elements, therefore return 0.
Constraints:
1 <= nums.length <= 104
0 <= nums[i] <= 109
Bucket-Sort based approach
Lets assume we are given 3 6 10 1, by applying bucket-sort algorithm we iterate through a given list and put items into their buckets. After that we iterate through buckets and while iterating track minimum and maximum values in the bucket. Minimum and maximum values of the bucket used to compare with neighbour bucket values. Means, while visiting each bucket we calculate difference between minimum of current bucket and maximum of previous bucket. The greatest difference among those differences is our answer.
In that example case we calculate 6 - 3 = 3 and then 10 - 6 = 4. Since 4 is the largest difference it will be the answer.
Bucket-sort is not applied as a whole, because in the purpose of this example is not a sort. Actual implementation of bucket-sort is un-nessary, only the concept is used. Because bucket-sort is good at clustering the distributed numbers. Though key-point here is to choose the right size of for the bucket. The number of total used buckets depends on the chosen bucket size. The claim here is that the bucket size should be equal or less than (maxVal-minVal) / (N - 1).
Anaylysis behind bucket size logic?
if we choose small bucket size, lets say 1 (where only 1 element per bucket), in that case we still solve the problem, but with un-effecient space allocation. If we choose big bucket size then, some required answers may locate inside the single bucket. It will require us to dig into each bucket and do another sorting operation (or recursively apply bucket-sort). In that case our runtime efficiency drops. To stay in the middle the medium bucket size need to be selected, which is (maxVal-minVal) / (N - 1)
By dividing the maxVal-minVal range length to total number of elements we are trying to promote uniform distribution of numbers over buckets.
Lets check it with example analysis:
When we have: 3 6 9 1
then bucket-size is: (maxVal-minVal) / (N - 1) => (9 - 1) / (4 - 1) => 2
since the size of the bucket is 2 we can calculate the number of buckets by (maxVal - minVal) / bucket_size which is 4:
b1(1) b2(3) b3(6) b4(9)
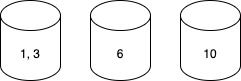
if we change the input little bit and say we have 10 instead of 9, then we have: 3 6 10 1
bucket-size: (maxVal-minVal) / (N - 1) => (10 - 1) / (4 - 1) => 9 / 3 = 3
following above formula we end up having three buckets:
b1(1, 3) b2(6) b3(10)
Solution Code
class Solution {
public int maximumGap(int[] nums) {
if (nums.length < 2) return 0;
int hi = 0, lo = Integer.MAX_VALUE, ans = 0;
for (int n : nums) {
hi = Math.max(hi, n);
lo = Math.min(lo, n);
}
int bSize = Math.max((hi - lo) / (nums.length), 1);
List<List<Integer>> buckets = new ArrayList<>();
for (int i = (hi - lo) / bSize; i >= 0; i--) {
buckets.add(new ArrayList<>());
}
for (int n : nums) {
buckets.get( (n - lo) / bSize ).add(n);
}
int curHi = 0;
for (List<Integer> buck : buckets) {
if (buck.isEmpty()) continue;
int prevHi = curHi > 0? curHi : buck.get(0), curLo = buck.get(0);
for (int n : buck) {
curHi = Math.max(curHi, n);
curLo = Math.min(curLo, n);
}
ans = Math.max(ans, curLo - prevHi);
}
return ans;
}
}