Topological Sort

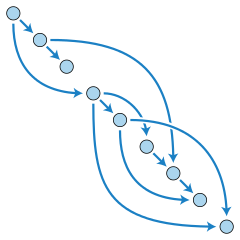
Idea

For a Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge (u,v), vertex u comes before v in the ordering.

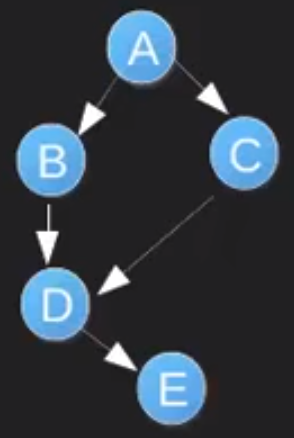
• For a DAG

• Topological sort is not unique:

  A B C D E

  A C B D E

Topological Sorting

Start with A and perform DFS, while not priting the path on the way. Go to deepest vertex and when there are no neighbours to go from the vertex (it can be by two reason: first is because it is a leaf node, second all neighbour nodes are already visited) set the vertex as visited and push it onto the stack.

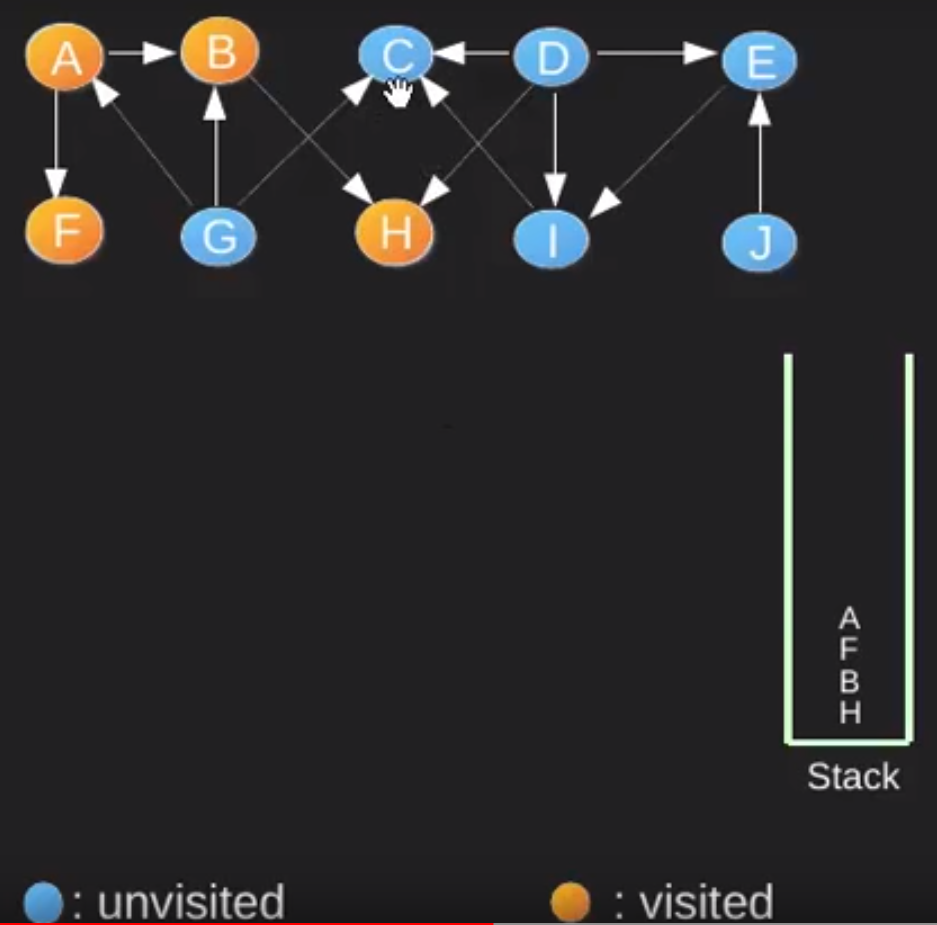
Continuing this process untill all nodes becomes visited and then perform pop operation from stack and print the poped elements from the stack.

Time Complexity

• O(V+E)

V is the number of vertices E is the number of Edges

Java Implementation

// A Java program to print topological sorting of a DAG
import java.io.*;
import java.util.*;
 
// This class represents a directed graph using adjacency
// list representation
class Graph
{
    private int V;   // No. of vertices
    private LinkedList<Integer> adj[]; // Adjacency List
 
    //Constructor
    Graph(int v)
    {
        V = v;
        adj = new LinkedList[v];
        for (int i=0; i<v; ++i)
            adj[i] = new LinkedList();
    }
 
    // Function to add an edge into the graph
    void addEdge(int v,int w) { adj[v].add(w); }
 
    // A recursive function used by topologicalSort
    void topologicalSortUtil(int v, boolean visited[],
                             Stack stack)
    {
        // Mark the current node as visited.
        visited[v] = true;
        Integer i;
 
        // Recur for all the vertices adjacent to this
        // vertex
        Iterator<Integer> it = adj[v].iterator();
        while (it.hasNext())
        {
            i = it.next();
            if (!visited[i])
                topologicalSortUtil(i, visited, stack);
        }
 
        // Push current vertex to stack which stores result
        stack.push(new Integer(v));
    }
 
    // The function to do Topological Sort. It uses
    // recursive topologicalSortUtil()
    void topologicalSort()
    {
        Stack stack = new Stack();
 
        // Mark all the vertices as not visited
        boolean visited[] = new boolean[V];
        for (int i = 0; i < V; i++)
            visited[i] = false;
 
        // Call the recursive helper function to store
        // Topological Sort starting from all vertices
        // one by one
        for (int i = 0; i < V; i++)
            if (visited[i] == false)
                topologicalSortUtil(i, visited, stack);
 
        // Print contents of stack
        while (stack.empty()==false)
            System.out.print(stack.pop() + " ");
    }
 
    // Driver method
    public static void main(String args[])
    {
        // Create a graph given in the above diagram
        Graph g = new Graph(6);
        g.addEdge(5, 2);
        g.addEdge(5, 0);
        g.addEdge(4, 0);
        g.addEdge(4, 1);
        g.addEdge(2, 3);
        g.addEdge(3, 1);
 
        System.out.println("Following is a Topological " +
                           "sort of the given graph");
        g.topologicalSort();
    }
}

Topological Sort Applications

• Build Systems: IDE such as Visual Studio, Eclipse. When we build our project the dependency between libraries and sub-projects should be considered. We cannot build the library before building and solving its dependencies.
• Advanced-Packaging Tool (apt-get): In Linux we use this tool in order simply install the applications and libraries into our OS. This tool also uses a dependency map to install.
• Task Scheduling
• Pre-requisite problems
• In a Blockchains

Usage in a Blockchain

It has been in used in a Dagger which is “memory-hard proof of work” algorithm. The main reason why memory hardness is important is to make the proof of work function resistant to specialized hardware such as FPGA or ASICs solutions.

The Dagger algorithm works by creating a directed acyclic graph (the technical term for a tree where each node is allowed to have multiple parents) with ten levels including the root and a total of 225 - 1 values. In levels 1 through 8, the value of each node depends on three nodes in the level above it, and the number of nodes in each level is eight times larger than in the previous. In level 9, the value of each node depends on 16 of its parents, and the level is only twice as large as the previous; the purpose of this is to make the natural time-memory tradeoff attack be artificially costly to implement at the first level, so that it would not be a viable strategy to implement any time-memory tradeoff optimizations at all. For more details about Dagger algorithm refer to link

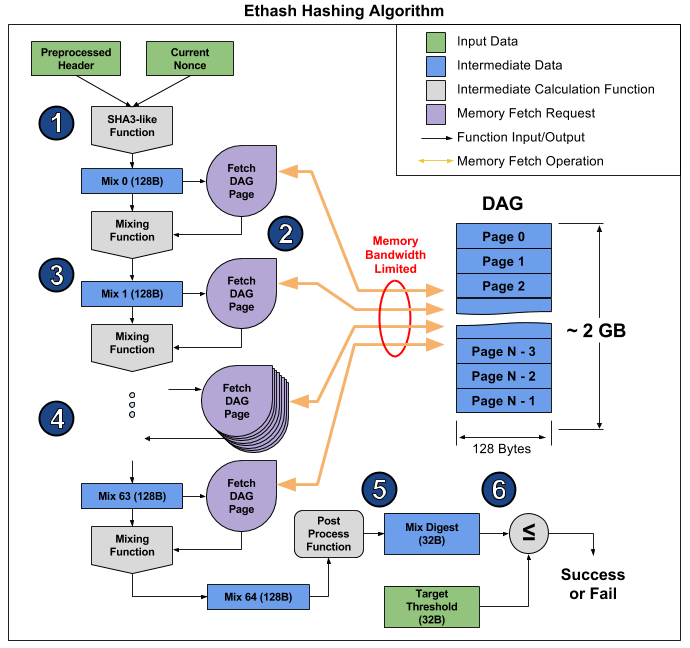
Why Is This Memory Hard?

Every mixing operation requires a 128 byte read from the DAG (See Figure above, Step 2). Hashing a single nonce requires 64 mixes, resulting in (128 Bytes x 64) = 8 KB of memory read. The reads are random access (each 128 byte page is chosen pseudorandomly based on the mixing function), so putting a small chunk of the DAG in an L1 or L2 cache isn’t going to help much, since the next DAG fetch will very likely yield a cache miss. Since fetching the DAG pages from memory is much slower than the mixing computation, we’ll see almost no performance improvement from speeding up the mixing computation. The best way to speed up the ethash hashing algorithm is to speed up the 128 byte DAG page fetches from memory. Thus, we consider the ethash algorithm to be memory hard or memory bound, since the system’s memory bandwidth is limiting our performance.