I have decided to describe this problem, because it is somehow has a good message for algorithm learners. Especially people who complains why should we learn the algorithms if we can just use the existing codes (or libraries) without diving into details. We need to learn algorithms to design our own by customizing them for our purpose. The purpose is usually solve more non-traditional problems which are not common. I have found this example particularly interesting.
Given
We are given an array and a number k where k is smaller than size of array. We need to find the k‘th largest (or smallest, that doesn’t matter) element in a given array. Given array is obviously not sorted.
Examples:
Input:
int arr[] = {12, 3, 5, 7, 19};
k = 4
Output:
result = 5
Input:
arr[] = {5, 6, 9, 12, 2, 1, 98, 526, 0, 25, 99, 99}
k = 4
Output:
result = 98
Solution by Sorting
Simple solution is to do sorting of the given array using O(Nlog(N)) where N is a size of the given array. After sorting we can just access by O(1) complexity to the *kth element and get the result
Solution by Quick Select
This solution is almost named after Quick Sort, because it uses the logic of quick sort algorithm. Shortly saying it uses QuickSort algorithm’s partition functionality and compares the current pivot’s position with the k. If they are match then we have no reason to continue, because the pivot gets its place and does not moves anymore. If the pivot’s new position is not equal to k then we have to choose a partition where the k index is located. After that perform partition on elements of choosen partition.
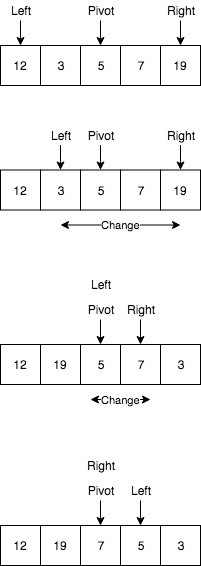
The meaning of pivot in QuickSort is to define the element to his position where all remaining small elements on one side and other large elements on the other side. So the pivot is static and doesn’t move anymore. That means if our kth element is in the small group then we continue on that side, otherwise we continue with large group. Continue this process until the pivot position is equal to k.
import java.util.Arrays;
public class KthLargets {
public static int quickSortSelect(int[] array, int kth) {
return quickSortSelect(array, 0, array.length - 1, kth);
}
public static int quickSortSelect(int[] array, int left, int right, int kth) {
if (left >= right) {
return -1;
}
int pivot = array[(left+right)/2];
int index = partition(array, left, right, pivot);
if (kth < index) {
return quickSortSelect(array, left, index-1, kth);
} else if (kth > index) {
return quickSortSelect(array, index, right, kth);
} else {
return kth;
}
}
public static int partition(int[] array, int left, int right, int pivot) {
while (left <= right) {
while (array[left] > pivot) {
left++;
}
while (array[right] < pivot) {
right--;
}
if (left <= right) {
swap(array, left, right);
left++;
right--;
}
}
return left;
}
public static void swap(int [] array, int left, int right) {
int tmp = array[left];
array[left] = array[right];
array[right] = tmp;
}
public static void main(String args[]) {
//int arr[] = {5,6,9,12,2,1,98,526,0, 25,99, 99};
int arr[] = {12, 3, 5, 7, 19};
System.out.println("given array: " + Arrays.toString(arr));
int ret = quickSortSelect(arr, 4);
System.out.println("kth largest element: " + arr[ret-1]);
}
}
Complexity
The worst case time complexity of this method is O(n^2), but it works in O(n) on average.