Breadth-first search systematically explores the edges of G graph to discover every vertex that is reachable from starting node S. The main purpose of BFS is to calculate the distance from S to each reachable vertex. If we are given two arbitrary nodes and asked for the distance between them, then the BFS is the standard solution. The algorithm works for both directed and un-directed graphs.

Pseudo-code and step-by-step representation from Cormen Book

G = (V, E) is represented using adjacency lists. It attaches several additional attributes to each vertex in the graph. Each vertex color is stored at u.color and the predcessor of u in the attributed u.p. If u has no predcessor then u.p = NIL. The attribute u.d holds the distance from the source s to vertex u computed by the algorithm. FIFO queue Q is used to manage the set of gray vertices.

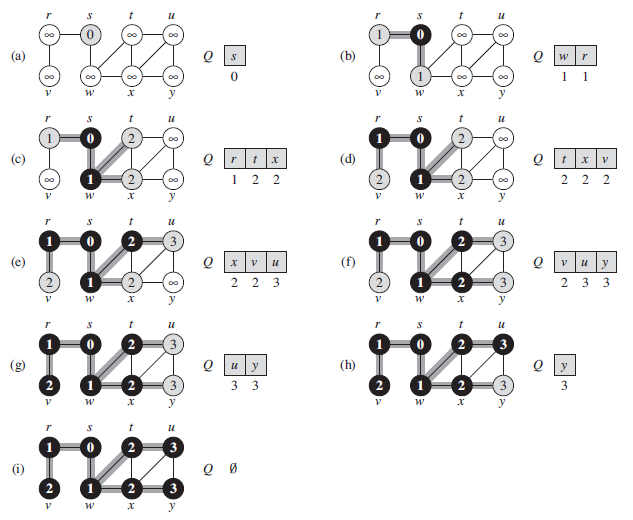
White color - not visited nodes
Gray color - about to be visited (keeping them in FIFO queue)
Black color - visited nodes

Intitialization with unlimited signature is needed to tell that node is impossible to reach from the starting s node. At the end of the BFS if still see some unlimited signs then there is no path from s to that node.

Implementation in Java

There are many implementations of BFS online. Here I would like to introduce the BFS that prints the levels while performs search. Even though the source code is little long, it is quite primitive.

public class BfsWithLevels {

    private int numOfVertices;
    private LinkedList<Integer> adj[];

    public BfsWithLevels(int n) {
        numOfVertices = n;
        adj = new LinkedList[numOfVertices];
        for (int i = 0; i < numOfVertices; i++) {
            adj[i] = new LinkedList<>();
        }
    }

    public void addEdge(int v, int w) {
        if (!adj[v].contains(w))
            adj[v].add(w);
        if (!adj[w].contains(v))
            adj[w].add(v);
    }

    void BFS(int s) {
        boolean visited[] = new boolean[numOfVertices];
        LinkedList<Integer> queue = new LinkedList<>();

        visited[s] = true;
        queue.add(s);

        boolean nextLineFlag = false;
        int levels = 1;

        System.out.print(levels + ") ");
        while (queue.size() != 0) {
            int curNode = queue.poll();
            System.out.print(curNode + " ");

            int curNodeNeighborsSize = adj[curNode].size();
            for (int i = 0; i < curNodeNeighborsSize ; i++) {
                int neighbor = adj[curNode].get(i);
                if (!visited[neighbor]) {
                    visited[neighbor] = true;
                    queue.add(neighbor);
                    nextLineFlag = true;
                }
            }
            if (nextLineFlag) {
                nextLineFlag = false;

                System.out.println();
                levels++;
                System.out.print(levels + ") ");
            }
        }
    }

    public static void main(String args[])
    {
        BfsWithLevels g = new BfsWithLevels(8);

        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 5);
        g.addEdge(3, 4);
        g.addEdge(4, 6);
        g.addEdge(4, 7);

        System.out.println("Following is Breadth First Traversal printing with levels number"+
                "(starting from vertex 0)");
        g.BFS(0);
    }
}