P and NP is the problem that always comes out while we are studying algorithms, and usually, it comes up at the end of any algorithms book. The reason it comes out at the latest pages is that it is quite an advanced topic.
P means the polynomial time, which is mathematically can be represented as x^k + x^3 + x ^2 + x + C = 0 where and has time complexity O(n^k). It is important to notice that k is not big for P-type of problems.
NP means the non-polynomial time and it has complexity O(k^n) which is way bigger than the complexity of P. Computer scientists try to optimize and come up with faster algorithmic solutions.
As a conclusion, we can efficiently solve P type of problems, while NP type of problems does not have an efficient algorithmic solution.
Millenium Prize Problems
- Birch and Swinnerton-Dyer conjecture
- Hodge conjecture
- Navier–Stokes equations
- P vs NP
- Poincaré conjecture
- Riemann hypothesis
- Yang-Mills theory
As we can see P vs NP is one of them and till now no-one could prove their equality or inequality. NP problems have such an interesting point where the problem with NP level has difficult to calculate. But if the solution is given then we can quickly compare and confirm it is correct. That is the beauty of mathematics and used in many areas of our daily life. Let’s show it in an example of sudoku which is also the NP-hard problem.
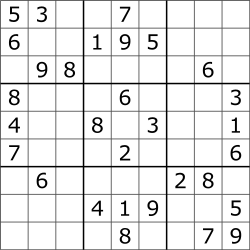
For given sudoku problem we can calculate the solution by manually playing sudoku, or by running with a simple computation machine which could try the possible variants and find the solution

Even our smartphone can calculate such sudoku problem in a matter of milliseconds. But if we increase the size of the sudoku board to 10000x10000, then the smartphone will not be enough to calculate the solution. If the solution of such board is given then easily can be confirmed.
The cryptography exploits this property very well, and almost all modern security solutions are based on the NP-hard problem.
Here what one of the MIT professors said about P-NP problem:
Does being able to quickly recognize correct answers mean there’s also a quick way to find them?
Categorization of the Problems
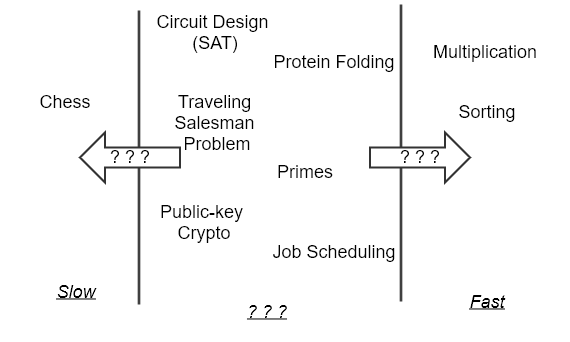
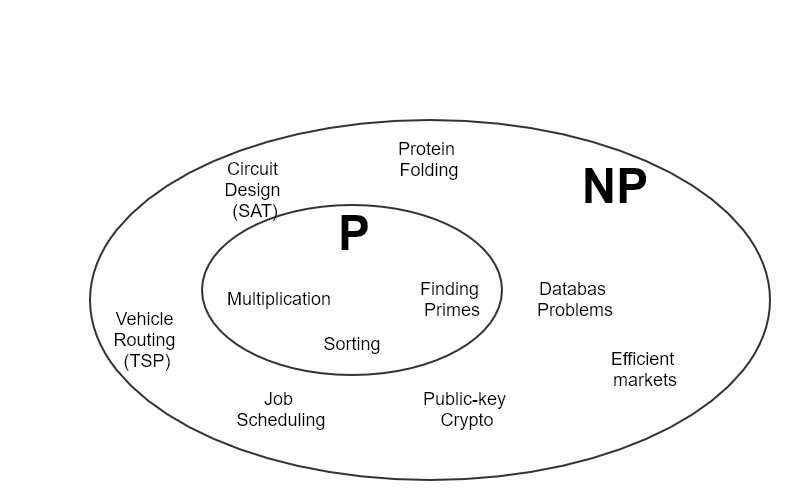
How can we distinguish is this problem P or NP type? And the answer can become a scientifically not easy and needed some mathematical skills. The most of the list of NP problems are already listed out and exists. If some problem has not been checked for being NP, then using some mathematical derivations it can be reduced to one of the existing NP problems. That is something like chain based proof. SAT (Boolean Satisfiability) is considered as a king among other NP problems. Because SAT is the first problem that was proven to be NP-complete by Cook–Levin theorem. Another mathematician Karp has shown and derived 21 NP-complete problems from Cook’s SAT thorem. The list of all known NP-complete problems can be refered from wikipedia.
Approximation Algorithms
What to do when the NP problem is met and we can’t do anything with it 1) Stick with small problems (use a exponential algorithm to solve) 2) Find special cases solvable in polynomial time 3) Find near-optimal solutions with approximation algorithms
- use clever heuristics
- linear program approximation
- randomization based solution
Definition
C cost of solution
C* optimal solution
p(n) = approximation ratio
minimization: C/C* <= p(n)
maximation: C*/C <= p(n)
Vertex Cover Approximation
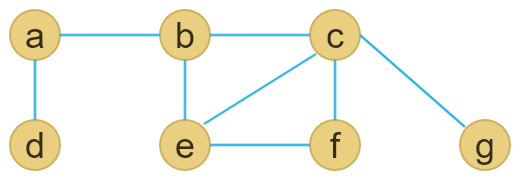
Find vertex cover V’ belong to V of G =(V, E) that is of minimum size
APPROX-VERTEX-COVER(G)
1 C = {}
2 E' = G,E
3 while E' != {}
4 let (u,v) be an arbitrary edge of E'
5 C = union(C, {u,v})
6 remove from E' every edge incident on either u or v
7 return C
proof: Let A be the set of edges chosen by algorithm |C| = 2 |A| |A| <= C* |C| <= 2 |C*|
TSP (Traveling Salesman Problem) Approximation
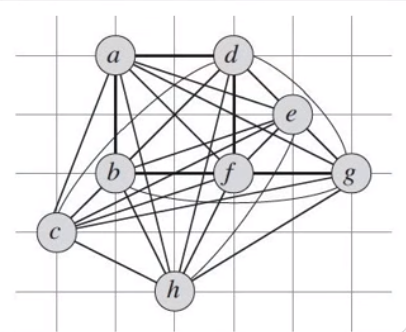
Cost function 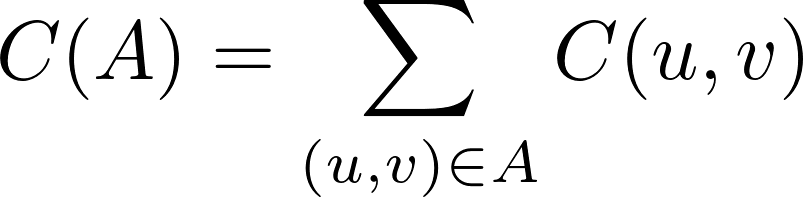
It is possible to get an approximation if the Traiangle equality is used
Triangle Inequality: C(u,v) <= C(u,w) + C(w,v)
APPROX-TSP-TOUR (G,C)
1 Select a vertex *r* in G.V to be a "root" vertex
2 Compute a minimum spanning tree T for G from root *r* using MST-PRIM(G, c, r)
3 let *H* be a list of vertices, ordered according to when they are first visited in a preorder tree walk of *T*
4 return the hamiltonian cycle *H*
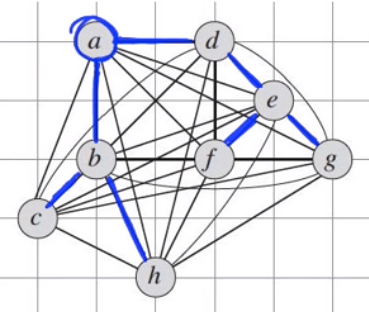
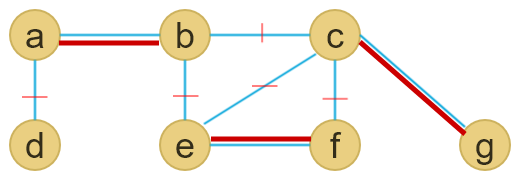
Next we traverse through the spanning tree by starting from root vertex a. In order to traverse the DFS(Depth-First-Search) can be used.
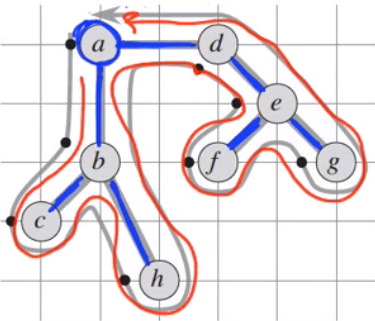
After traversing here what we get :
a - b - c - b - h - b - a - d - e - f - e - g - e - d - a
In order to not pay the twise of the cost of visiting each vertex we should apply the triangle inequality rule.
a - b - c - h - d - e - f - g - a
That cycle is the result of applying approximate algorithm, but it does not mean it is the really optimal solution. It is called near optimal solution.
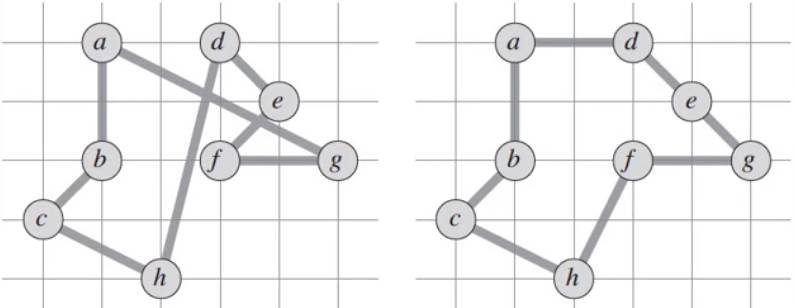
Here we can see approximate solution (on the left) versus optimal soltuion (on the right)
References: https://www.youtube.com/watch?v=hdch8ioLRqE