It has been such a long time since I didn’t work on graphs and trees. Here it is I’m back. This task is quite a simple one even though it is assigned a medium level of difficulty. The original task definition is given hackerrank.
Solution Description
The reason it is assigned medium level is because You have to implement two In-order traversals on binary tree to solve this problem:
- In-order traverser should do the swapping depend on the depth of the current node. (the depth should be a multiple of the given k)
- In-order traverse and print the current status of the binary tree
First of all lets define the Node data structure. Basically Binary tree data structure contains left, right and data values. But in this task we have to do swapping of the left and right branches of the tree based on the depth of the current node. That is why it is important to keep track of the depth of current node. That is why we have added additional field of depth for basic binary tree data structure:
static class Node {
int index;
int depth;
Node left;
Node right;
public Node(int index, int depth, Node left, Node right) {
this.depth = depth;
this.index = index;
this.left = left;
this.right = right;
}
}
Before those In-order traverser functios are added we have to implement the reading of the tree. Reading tree from the input pairs should be performed in a top-to-down and left-to-right fashion.
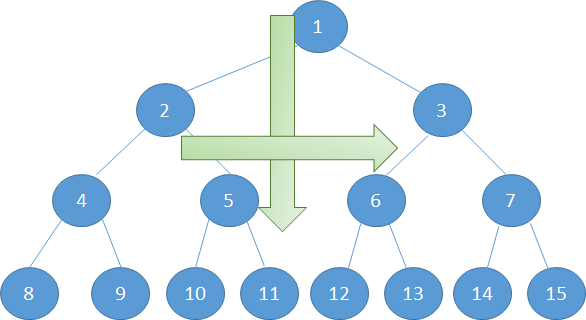 .
.
The above Binary tree is formed from input such as given below. The root node has an index equal to 1. It is default for all birnary trees in this example, that is why input does not contain root index. First number represents left child index while second number represents right child node index.
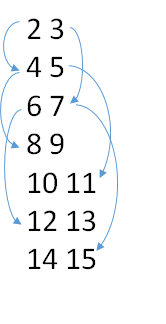
Reading the 2D array and forming the binary tree is performed by following code:
int N = 0;
while (N < numOfNodes) {
cur = nodes.poll();
int leftData = indexes[N][0];
int rightData = indexes[N][1];
cur.left = (leftData==-1)? null: new Node(leftData, cur.depth+1, null, null);
cur.right = (rightData==-1)? null: new Node(rightData, cur.depth+1, null, null);
if (cur.left != null && cur.left.index != -1)
nodes.offer(cur.left);
if (cur.right != null && cur.right.index != -1)
nodes.offer(cur.right);
N++;
}
Finally when we are done with reading the binary tree, now its time to perform In-order traversing. Back in University we have learned an easy way of remembering the In-order traversal by calling it LRR (Left-Root-Right) traversal. It is really easy way of remembering the whole algorithm. First we just keep diving into the left node, when there is nothing left we go to root. After processing root node (in our case printing and depth comparison) we go to right node, and then again going Left nodein there. Really simple algorithm but very powerful.
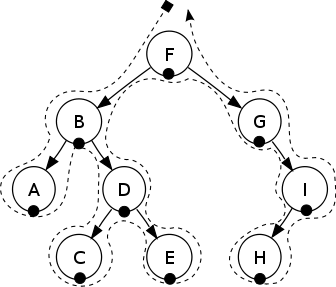
The whole algorithm boils down into few lines of code:
static void printInOrder(Node cur, List<Integer> result) {
if (cur == null) {
return ;
}
printInOrder(cur.left, result);
result.add(cur.index);
printInOrder(cur.right, result);
}
The current node should be checked to not being null, we call it stopper. Because in dynamic programming that is important to know when to stop :) Another function swapInOrder() function has been implemented in similar fashion where at the every node it checks the depth level and performs the swapping of the left and right branches.
Solution (Java)
import java.io.*;
import java.math.*;
import java.text.*;
import java.util.*;
import java.util.regex.*;
public class Solution {
/*
* Complete the swapNodes function below.
*/
static class Node {
int index;
int depth;
Node left;
Node right;
public Node(int index, int depth, Node left, Node right) {
this.depth = depth;
this.index = index;
this.left = left;
this.right = right;
}
}
static void printInOrder(Node cur, List<Integer> result) {
if (cur == null) {
return ;
}
printInOrder(cur.left, result);
//System.out.print(cur.index + " ");
result.add(cur.index);
printInOrder(cur.right, result);
}
static void swapInOrder(Node cur, int depth, int k) {
if (cur == null) {
return ;
}
swapInOrder(cur.left, depth + 1, k);
//System.out.print("cur.index: " + cur.index);
swapInOrder(cur.right, depth + 1, k);
if (depth >=k && depth % k == 0 ) {
Node tmp = cur.left;
cur.left = cur.right;
cur.right = tmp;
}
}
static int[][] swapNodes(int[][] indexes, int[] queries) {
int numOfNodes = indexes.length;
int numOfQueries = queries.length;
int[][] result = new int[numOfQueries][numOfNodes];
Node root = new Node(1, 1, null, null);
Node cur = root;
Queue<Node> nodes = new LinkedList<Node>();
nodes.offer(cur);
int N = 0; // = numOfNodes;
while (N < numOfNodes) {
cur = nodes.poll();
int leftData = indexes[N][0];
int rightData = indexes[N][1];
//System.out.println("left,right: " + leftData + " " + rightData + " cur: " + cur );
cur.left = (leftData==-1)? null: new Node(leftData, cur.depth+1, null, null);
cur.right = (rightData==-1)? null: new Node(rightData, cur.depth+1, null, null);
if (cur.left != null && cur.left.index != -1)
nodes.offer(cur.left);
if (cur.right != null && cur.right.index != -1)
nodes.offer(cur.right);
N++;
}
//TODO: till here we have formed the tree, [not checked yet]
for (int i = 0; i < numOfQueries; i++) {
swapInOrder(root, 1, queries[i]);
List<Integer> res = new ArrayList();
printInOrder(root, res);
result[i] = res.stream().mapToInt(r->r).toArray();
}
return result;
}
private static final Scanner scanner = new Scanner(System.in);
public static void main(String[] args) throws IOException {
BufferedWriter bufferedWriter = new BufferedWriter(new FileWriter(System.getenv("OUTPUT_PATH")));
int n = Integer.parseInt(scanner.nextLine().trim());
int[][] indexes = new int[n][2];
for (int indexesRowItr = 0; indexesRowItr < n; indexesRowItr++) {
String[] indexesRowItems = scanner.nextLine().split(" ");
for (int indexesColumnItr = 0; indexesColumnItr < 2; indexesColumnItr++) {
int indexesItem = Integer.parseInt(indexesRowItems[indexesColumnItr].trim());
indexes[indexesRowItr][indexesColumnItr] = indexesItem;
}
}
int queriesCount = Integer.parseInt(scanner.nextLine().trim());
int[] queries = new int[queriesCount];
for (int queriesItr = 0; queriesItr < queriesCount; queriesItr++) {
int queriesItem = Integer.parseInt(scanner.nextLine().trim());
queries[queriesItr] = queriesItem;
}
int[][] result = swapNodes(indexes, queries);
for (int resultRowItr = 0; resultRowItr < result.length; resultRowItr++) {
for (int resultColumnItr = 0; resultColumnItr < result[resultRowItr].length; resultColumnItr++) {
bufferedWriter.write(String.valueOf(result[resultRowItr][resultColumnItr]));
if (resultColumnItr != result[resultRowItr].length - 1) {
bufferedWriter.write(" ");
}
}
if (resultRowItr != result.length - 1) {
bufferedWriter.write("\n");
}
}
bufferedWriter.newLine();
bufferedWriter.close();
}
}