Algorithms, Divide-and-conquer

Posted on | In |

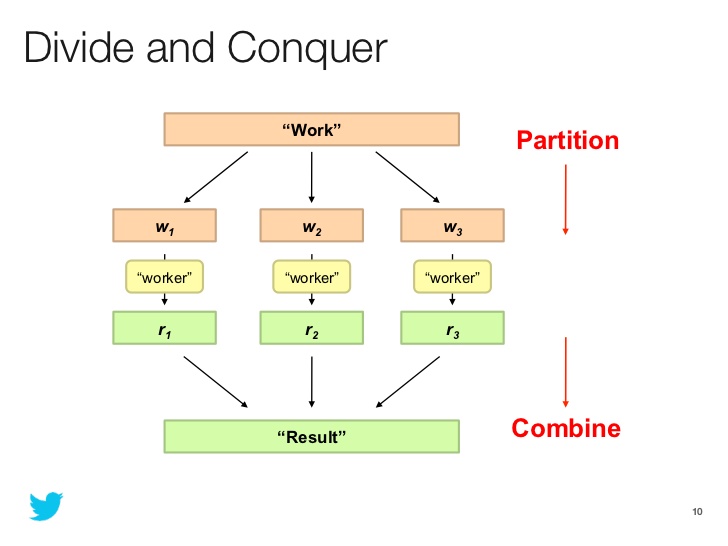
In a paradigm of divide-and-conquer we solve the problem recursively, applying three basic steps at each level of the recursion:

  • Divide the problem into a number of subproblems that are smaller instances of the same problem
  • Conquer the subproblems by solving them recursively. If the subproblem sizes are small enough (bottom out)
  • Combine the solutions to the subproblems into the solution for the original problem

NoImage

A recurrence is an equation or inequality that describes a function in terms of its value on smaller inputs.

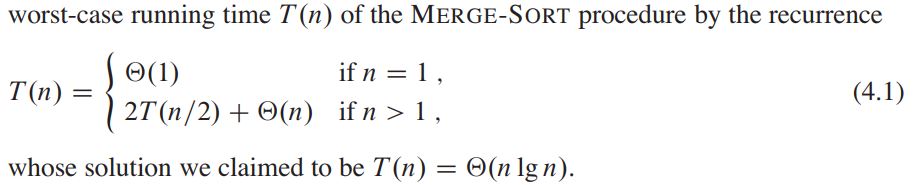
NoImage

There are three methods for solving recurrences - that is, for obtaining “O” bounds on the solution:

  • In the substitution method, we guess a bound and then use mathematical induction to prove our guess correct
  • The recursion-tree method converts the recurrence into a tree whose nodes represent the costs incurred at various levels of the recursion. We use techniques for bounding summations to solve the recurrence
  • The master method provides bounds for recurrences of the form

T(n) = aT(n/b) + f(n)

where a >= 1, b > 1 and f(n) is a given function.

The maximum-subarray problem

Finding a maximum-subarray is quite popular problem around, and it has multiple solutions: brute-force, divide-and-conquer and kadane.

Divide-and-conquer suggests that we divide the subarray into two subarrays of as equal size as possible. We find the midpoint, say mid, of the subarray, and consider the subarrays A[low … mid] and A[mid + 1 … hight] must lie in exactly one of the following places:

  • entirely in the subarray A[low .. mid], so that low <= i <= j <= mid
  • entirely in the subarray A[mid + 1 .. high], so that mid < i <= high
  • crossing the midpoint, so that low <= i <= mid < j <= high
FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high):
left-sum = -infinity
sum = 0
for i = mid downto low
   sum = sum + A[i]
   if sum > left-sum
      left-sum = sum
      max-left = i
right-sum = -infinity
sum = 0
for j = mid + 1 to high
   sum = sum + A[j]
   if sum > right-sum
      right-sum = sum
      max-right = j
return (max-left, max-right, left-sum + right-sum)

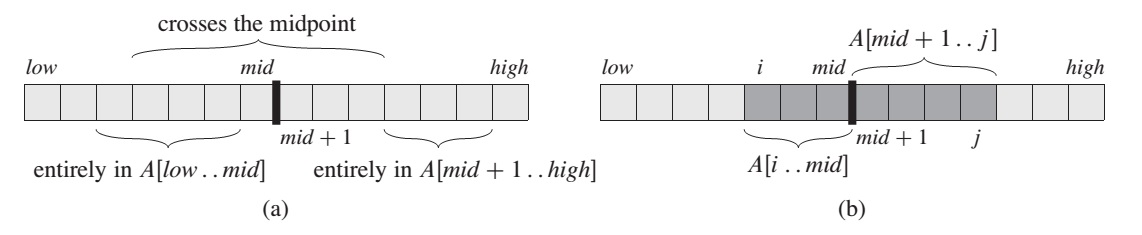
NoImage

  • (a) Possible locations of subarrays of A[low..high]: entirely in A[low..mid], entirely in A[mid + 1..high], or crossing the midpoint mid
  • (b) Any subarray of A[low..high] crossing the midpoint comprises two subarrays A[i..mid] and A[mid + 1 .. j], where low <= i <= mid and mid < j <= high

With a linear-time FIND-MAX-CROSSING-SUBARRAY procedure in hand, we can write pseudocode for a divide-and-conquer algorithm to solve the maximum-subarray problem:

FIND-MAXIMUM-SUBARRAY(A, low, high):
if high == low
   return (low, high, A[low])                // base case: only one element
else
   mid = floor((low + high)/2)
   (left-low, left-high, left-sum) = FIND-MAXIMUM-SUBARRAY(A, low, mid)
   (right-low, right-high, right-sum) = FIND-MAXIMUM-SUBARRAY(A, mid+1, high)
   (cross-low, cross-high, cross-sum) = FIND-MAXIMUM-CROSSING-SUBARRAY(A, low, mid, high)
   if left-sum >= right-sum and left-sum >= cross-sum
      return (left-low, left-high, left-sum)
   elseif right-sum >= left-sum and right-sum >= cross-sum
      return (right-low, right-high, right-sum)
   else return (cross-low, cross-high, cross-sum)

The initial call FIND-MAXIMUM-SUBARRAY(A, 1, A.length) will find a maximum subarray of A[1..n]

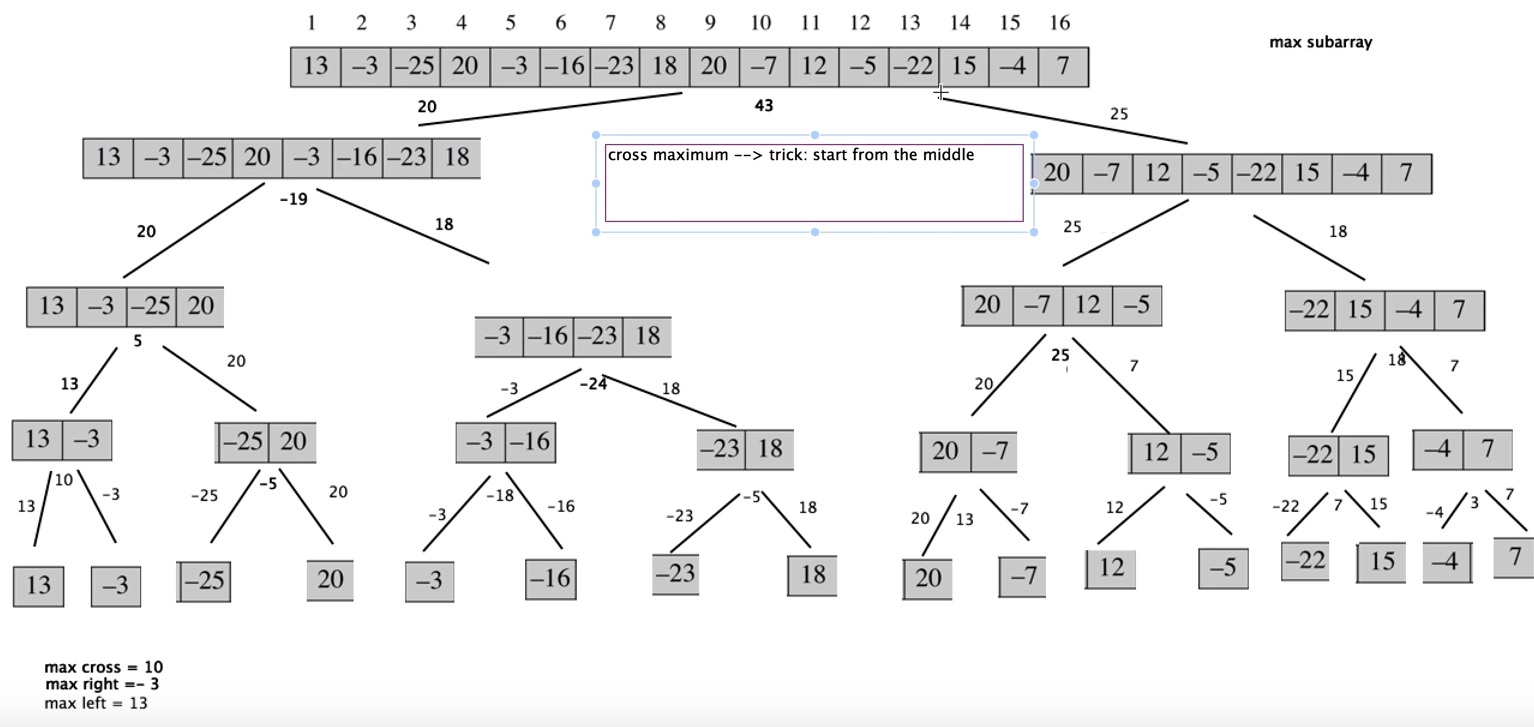
NoImage

The find-maximum-subarray is explained in here (step-by-step-running)[https://www.youtube.com/watch?v=t57Qr3vgi54]

You can try to solve the hackerRank problem for testing this method