The quicksort algorithm has a worst-case running time of O(n^2) on an input array of n numbers, and worst case happens when the array is sorted in descending order. Despite a worst-case running time, quicksort is often the best practical choice for sorting. Its average expected running time is O(n log n), and it has an advantage of sorting in place.
Description of Quicksort
It uses the divide-and-conquer paradigm:
- Divide: Parititon the array A[p..r] into two sub-arrays A[p..q-1] and A[q+1..r] such that each element of A[p..q-1] <= A[q] <= A[q+1..r]
- Conquer: Sort the two subarrays A[p..q-1] and A[q+1..r] by recursive calls to quicksort
- Combine: Because the subarrays are already sorted, no work is needed to combine them
QUICKSORT(A, p, r):
if p < r
q = PARTITION(A, p, r)
QUICKSORT(A, p, q - 1)
QUICKSORT(A, q + 1, r)
Initial call: QUICKSORT(A, 1, A.length)
Partitioning the array
PARTITION(A, p, r)
x = A[r]
i = p - 1
for j = p to r - 1
if A[j] <= x
i = i + 1
exchange A[i] with A[j]
exchange A[i + 1] with A[r]
return i + 1
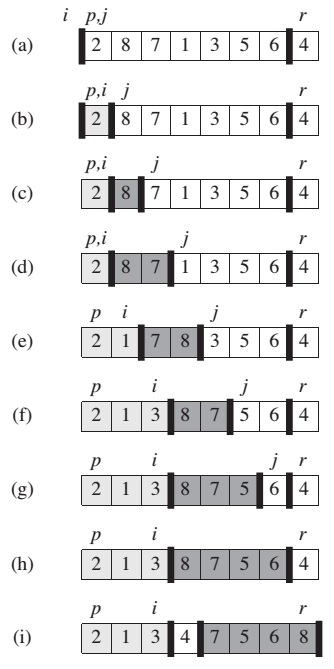
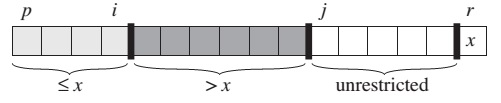
As a procedure runs, it partitions the array into four regions.
Best-case partitioning occurs when PARTITION produces two subproblems, each of size no more than n/2, since one is of size floor(n/2) and one of size ceil(n/2)-1. In this case quicksort runs much faster, with recurrence time:
T(n) = 2T(n/2) + O(n)
this recurrence has the solution T(n) = O(n lg n) Average-case running time of quicksort is much closer to the best case than to the worst case.
A Randomized version of quicksort
Instead of always using A[r] as the pivot, we will select a randomly chosen element from the subarray A[p..r]. We do so by first exchanging element A[r] with an element chosen at random from A[p..r]. By randomly sampling the range p,…,r we ensure that the pivot element x = A[r] is equally likely to be any of the r-p+1 elements in the subarray.
RANDOMIZED-PARTITION(A, p, r)
i = RANDOM(p, r)
exchange A[r] with A[i]
return PARTITION(A, p, r)
Randomized look of the quicksort will be as follows:
if p < r
q = RANDOMIZED-PARTITION(A, p, r)
RANDOMIZED-QUICKSORT(A, p, q-1)
RANDOMIZED-QUICKSORT(A, q+1, r)
The quicksort procedure was invented by Hoare. Hoare’s version appears in the “Introduction to Algorithms” book [Cormen] at Problem 7-1.